图论问题渗透整个计算机科学,解决图论问题的相关算法对计算机科学领域至关重要。最基本的是对图的遍历与搜索,不过首先要讨论的是如何将图表示为可用的数据结构。
图的表示
算法导论中介绍了图的两种常用表示方法,分别是邻接链表和邻接矩阵,在面向对象编程中,还有一种常用表示方法,即对象和指针(引用),也有称为边列表(edge list)。
根据图的定义,有向图和无向图均由一个顶点集合和这个顶点集合$V$中顶点间是否连接以及是否有向所构成的一个边集合$E$组成,定义图为顶点集和相应边集的二元组\(G = (V, E)\),对图的三种表示形式只是对这一定义在编程语言或者说是内存中的表示形式。其中对象和指针(边列表)表示方法是最接近原始的定义的,即顶点集合与边集合。
将图的n个顶点使用0到n-1的序号进行编号,下面分别对三种表示方法进行描述,并比较其在如下几个方面的不同:
- 内存占用
- 判断两个顶点是否相连(即连接这两个顶点的边是否存在)的时间复杂度
- 寻找一个顶点的所有邻居顶点
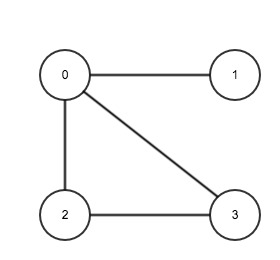
对象指针(边列表)
- 对象指针
Set<Vertex> vertexSet = new HashSet();
Set<Edge> edgeSet = new HashSet();
Vertex a = new Vertex(0);
Vertex b = new Vertex(1);
Vertex c = new Vertex(2);
Vertex d = new Vertex(3);
vertexSet.add(Arrays.asList({}));
edgeSet.addAll(Arrays.asList({new Edge(a, b),
new Edge(a, c),
new Edge(a, d),
new Edge(b, a),
new Edge(c, a),
new Edge(c, d),
new Edge(d, a),
new Edge(d, c)}));
- 边列表 边列表中的每个元素表示两个相邻顶点构成的边,其中顶点用其序号给出。
int[][] edgeList = {{0, 1}, {0, 2}, {0, 3}, {1, 0}, {2, 0}, {2, 3}, {3, 0}, {3, 2}};
邻接链表
邻接链表中第$i$个元素包含与顶点$v[i]$相邻的其它顶点的序号:
int[][] adjList = {
{1, 2, 3},
{0},
{0, 3},
{0, 2}
}
邻接矩阵
矩阵行列的序号对应顶点在数组中的序号,矩阵中行$i$与列$j$对应元素为1,表示顶点$v[i]$与$v[j]$相邻,为0表示不相邻。
int[][] adjMatrix = {
{0, 1, 1, 1},
{1, 0, 0, 0},
{1, 0, 0, 1},
{1, 0, 1, 0}
}
顶点集合中的顶点都是独立的,其连接信息在边中,对于内存占用仅考虑边集的内存占用,设一个顶点占用的空间为1,对于图$G = (V, E)$,共有$|V|$个顶点,$|E|$条边:
| 表示方法 | 空间复杂度 | 判断顶点相连的时间复杂度 | 寻找顶点所有邻居的时间复杂度 |
|---|---|---|---|
| 对象与指针(边列表) | \(O(2\lvert E\rvert)\) | $O(\lvert E\rvert)$ | $O(\lvert E\rvert)$ |
| 邻接链表 | $O(\lvert E\rvert)$ | $O(\lvert E\rvert)$ | $O(1)$ |
| 邻接矩阵 | $O(\lvert V\rvert^2)$ | $O(1)$ | $O(\lvert V\rvert)$ |
对象与指针表示法与邻接列表的空间和时间复杂度比较接近,因此这里主要将邻接列表与邻接矩阵作具体的比较。从上表可以看出,对于稀疏图,即$|E| « |V|^2$的图,使用邻接列表更加紧凑。而对于稠密图,即$|E|$接近$|V|^2$的情况下,那么更倾向于使用邻接矩阵表示法。对于判断两个顶点是否相连,邻接矩阵是最高效的。对于寻找一个顶点的所有邻居,邻接列表是最高效的。
对于权重图或者图的属性的表示,可以根据需要对上述表示方法进行扩展。其中对象与指针的表示方法是最容易扩展的,只需要将权重或者其它属性作为对象的实例变量即可。而其它表示方法可能需要定义专门的数据结构以存放额外的信息。
图的搜索
最简单的图算法就是对图的搜索,它是许多其它更复杂图算法的基础。一般分为广度优先搜索(breadth-first search)和深度优先搜索(depth-first search)。在搜索中第一次遇到一个结点称该结点被“发现”,下面使用邻接链表的方式来表示图,即可以是有向图也可以是无向图。
广度优先搜索(BFS)
广度优先搜索是最简单的图搜索算法之一,也是许多重要图算法的原型,如Prim的最小生成树算法和Dijkstra的单源最短路径都使用了类似广度优先搜索的思想。
广度优先搜索的基本思想是从一个源结点s开始,在发现一个结点v后优先访问其邻接链表v.adj中的结点,使该结点称为其邻接列表中还未被发现的结点的父节点,然后再依次访问v.adj中以v为父结点的所有结点的邻接链表中的结点,依次类推,直到所有结点都被发现。最终会形成以起始结点s为根的一棵广度优先搜索树。
这一过程中为了避免重复访问已发现的结点,将未被访问发现的结点标记为白色,已访问结束的结点标记为黑色,还可以设置一个中间状态即正在被访问的结点为灰色,所谓正在被访问即正在遍历该结点邻接链表中的结点。
深度优先搜索(DFS)
深度优先搜索的基本思想是在发现一个结点v后,再从v的邻接链表v.adj中某个未被发现的结点开始u,使v成为u的父结点,重复这一过程直到所发现的一个结点没有还未发现的结点为止。最终会形成一个由多棵深度优先树构成的深度优先森林。
同样为了避免重复访问已发现的结点,将未被访问的结点标记为白色,访问结束的结点标记为黑色,正在访问中的结点为灰色,这里的正在访问指对以该结点为根的深度优先树的访问还未结束。